Hydrogen Atom Wave Functions
Sunday, March 6, 2022
Three-Dimensional Schrödinger Equation
In order to fully describe the hydrogen atom, we must use the three-dimensional Schrödinger equation. In Cartesian coordinates it is
The usual way to solve such an equation would be to separate the variables by replacing a function of the three variables, , as a product of three functions, . However, the equation for Coulomb potential energy in three-dimensions, is not separable.
Instead, it is much easier to use spherical polar coordinates . This results in the Schrödinger equation becoming
Note that the wave function is now written in terms of , , and . Since the potential energy is described by only, the wave function can be factored as
where is the radial function, is the polar function, and is the azimuthal function.
The quantum state of a particle whose potential energy is determined by only can be described as having angular momentum quantum numbers and . The polar and azimuthal functions above can be solved using basic trigonometric functions, and the radial function is solved using the following differential equation:
Note: the mass, , here is the reduced mass of the proton-electron system.
Quantum Numbers and Wave Functions
Solving the three-dimensional Schrödinger equation results in three indices (or labels) which describe solutions (just like how the single index emerged when solving the one-dimensional version). These are the quantum numbers that describe the solutions.
One is , the principle quantum number, which can take on values . Another is the angular momentum quantum number, , which can have values . The third is the magnetic quantum number, , which can have values .
The principle quantum number () is the same as the quantum number found using the Bohr model, and can be used to quantize the energy levels:
Quantum numbers in radial, polar, and azimuthal functions
Using the quantum numbers, the three-dimensional wave function can be separated as such:
Degeneracy
The energy level has four different sets of quantum numbers: , , , and . This means the energy level is degenerate. In general, the level with principle quantum number has a degeneracy of .
Even though degenerate combinations have the same energy, different combinations of quantum numbers do not have exactly the same energy (it differs by about eV). Additionally, the transitions between levels depends on the degeneracy. Finally, each combination of quantum numbers corresponds to a very different wave function, representing very different state of motion of the electron. The degeneracy of the energy level influences how the atom can form bonds, for instance.
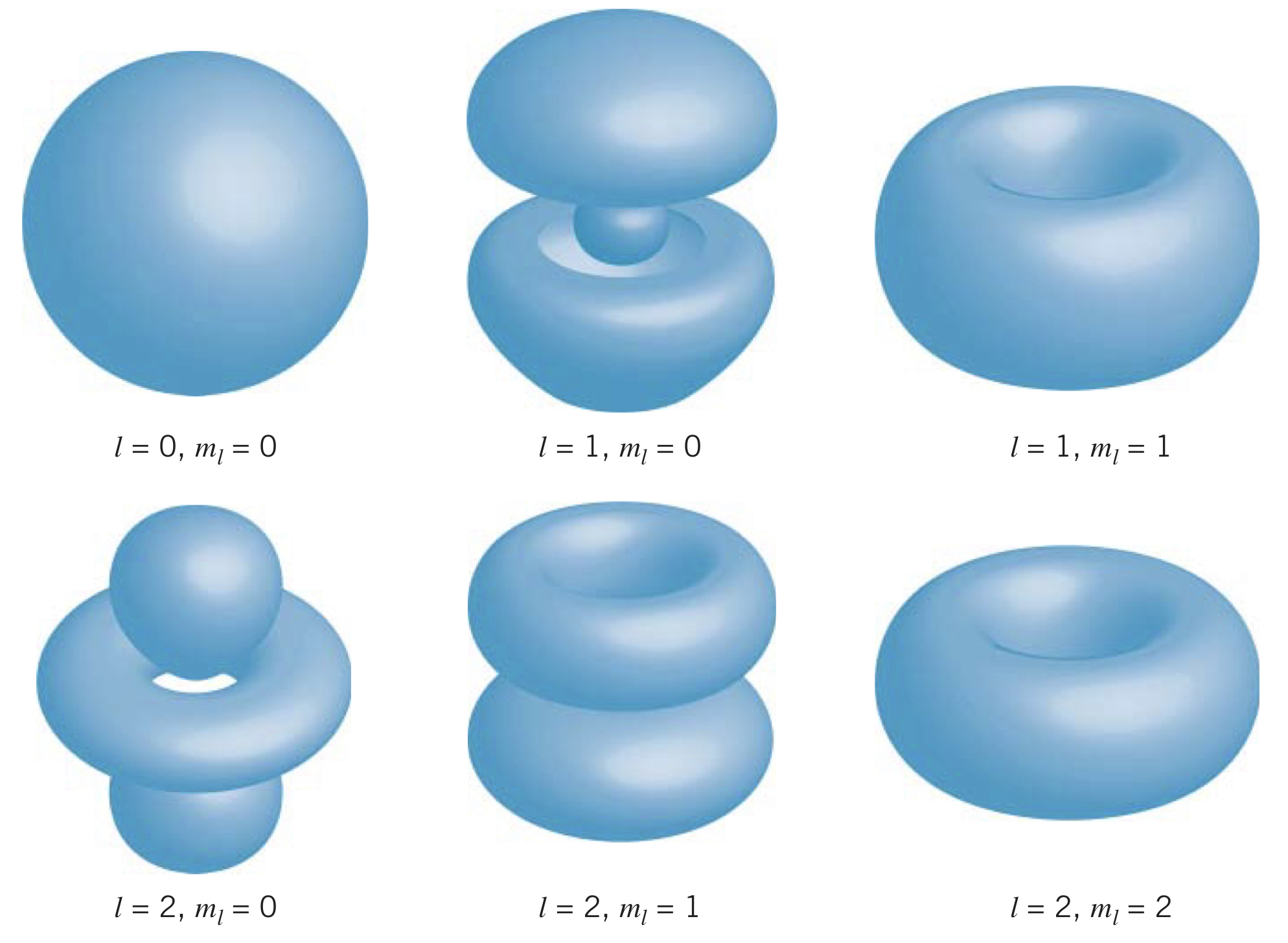
Probability Densities
Using the square of the three-dimensional wave function, gives us the volume probability density at the location . By using the volume element, , in spherical polar coordinates, we can find the probability the electron is within a volume element:
Some examples of probability density functions can be seen below, where the uncertainty in the electron's position is visually represented as a volume.