Molecular Rotations
Friday, March 18, 2022
Rotations in Quantum Mechanics
In classical physics, a rotor with rotational inertial has rotational kinetic energy , where is the rotational angular momentum. There is no obvious analogy in quantum mechanics, but we can imagine a particle of mass rotating on the end of a rod of length . However, in quantum mechanics it is not possible to have rotations in a fixed plane (due to the uncertainty relationship), so we instead imagine a particle confined to move in three dimensions on a sphere of radius .
The resulting energies take the form
where is the angular momentum quantum number. The rotational levels have energies (note: not equally spaced).
We can then find the kinetic energy by replacing classical angular momentum with quantum angular momentum . Note: is used to represent the angular momentum quantum number of a system whereas is used to represent the angular momentum quantum number of a particle.
Much like the vibrational states, there is a selection rule for rotational states too:
Rotating Diatomic Molecules
Imagine a diatomic molecule whose center of mass is at the origin ().
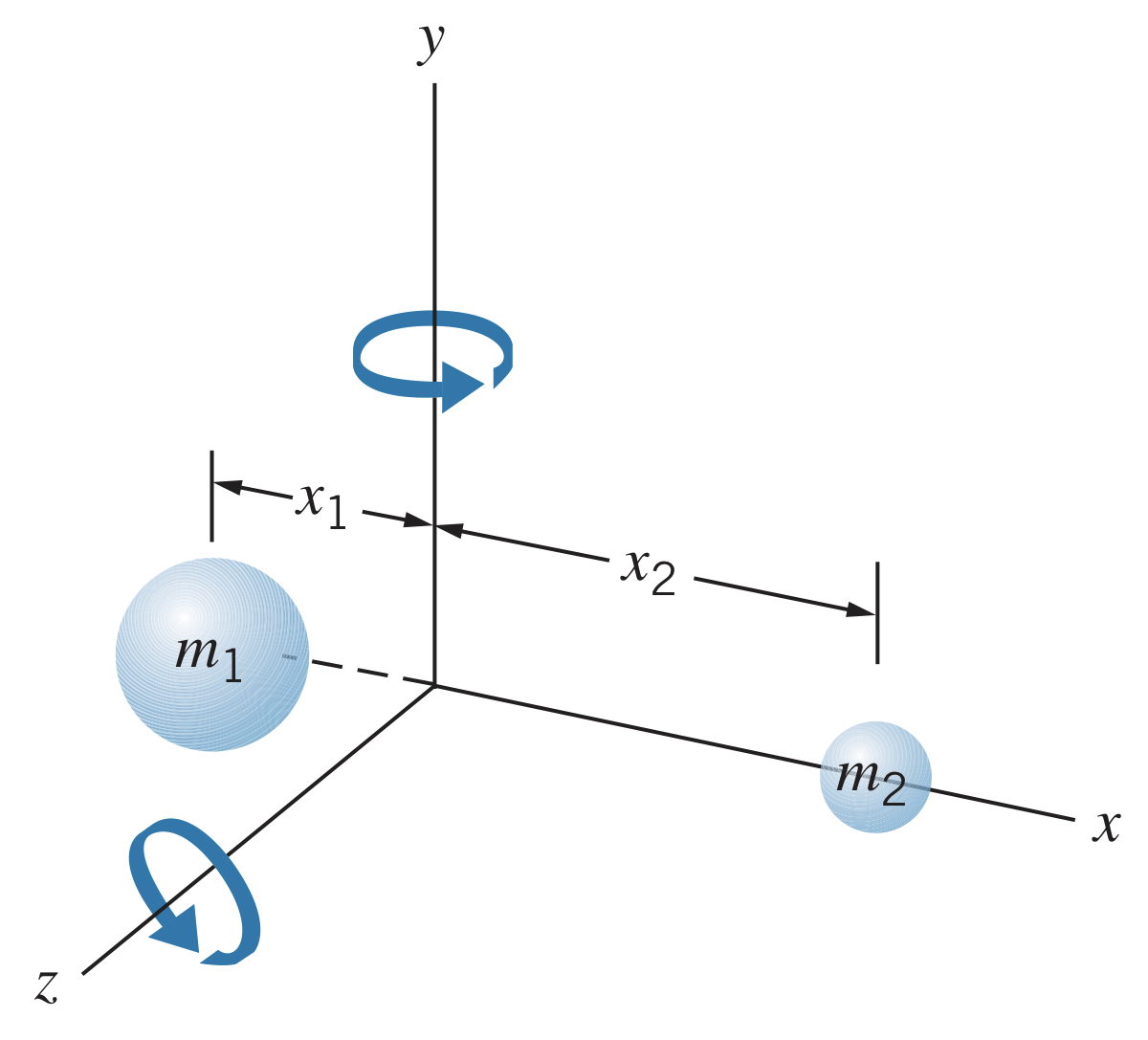
The rotational inertia is , or, using the reduced mass and equilibrium separation :
Plugging this into the energy states, we get
where is the rotational parameter, defined for diatomic molecules as
The energy absorbed or emitted must follow the selection rule and transition between adjacent levels, so
Here again we see that the spacing between energy levels depends on itself rather than being equally spaced as it is in vibrational transitions. Emitted photons can have energies .