Molecular Vibrations
Friday, March 18, 2022
Vibrations in Quantum Mechanics
In a classical system, a vibrating system as an object of mass on a spring of force constant has an oscillation frequency . It has an associated energy , and a maximum amplitude of , meaning it has a (constant) total energy of .
Quantum oscillators have only certain allowed energies:
The ground-state energy () is therefore , and each energy level is spaced by . Note: there is no energy state where (since this would have a displacement of exactly zero and momentum of exactly zero, violating the uncertainty principle). Instead, the minimum energy is often called the zero-point energy.
Allowed transitions
The oscillator can absorb or emit radiation to jump to different states. However, these states must differ in by exactly one unit. This is called a selection rule.
Vibrating Diatomic Molecules
Imagine a diatomic molecule oscillating.
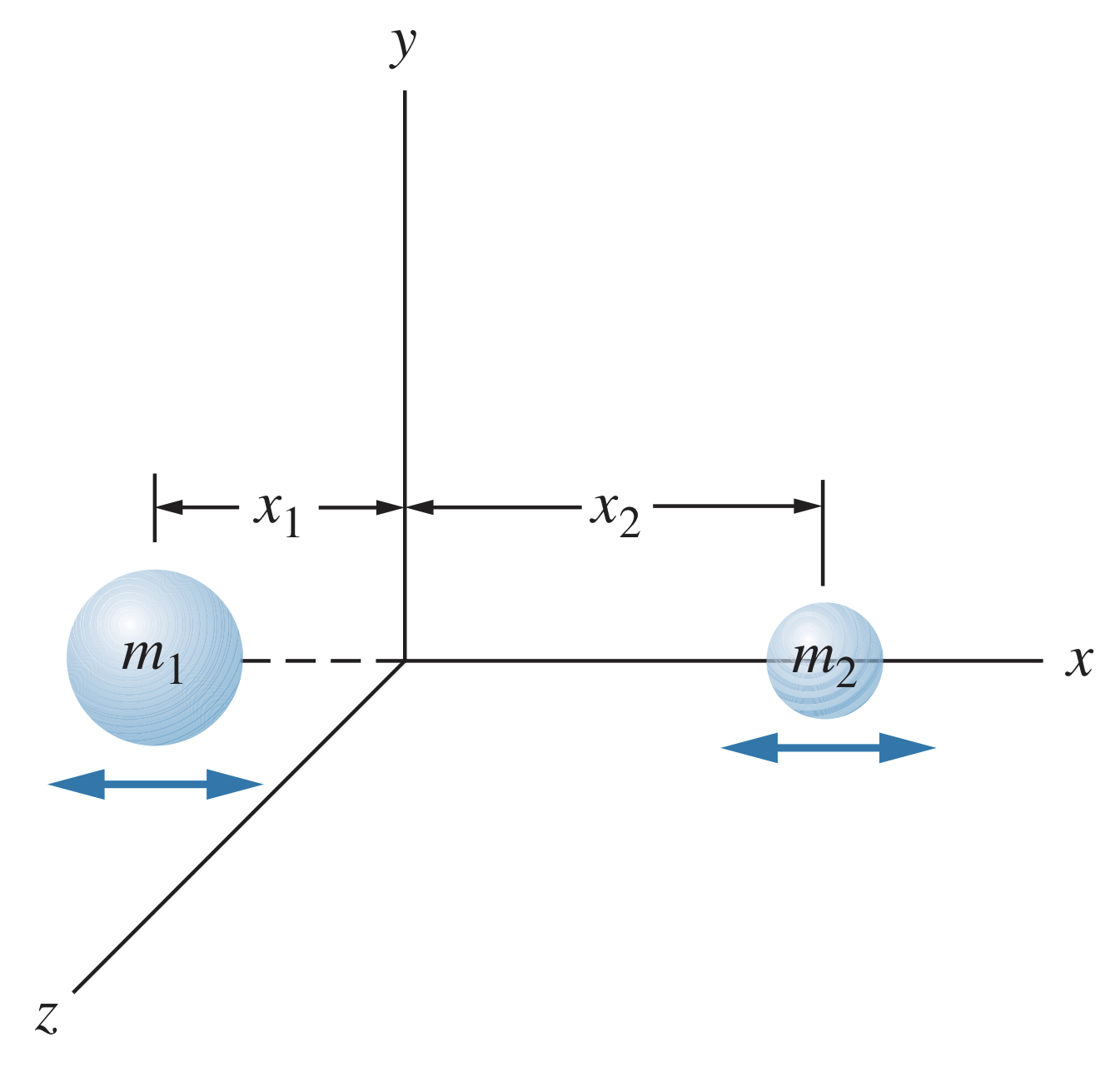
The two atoms have masses and and effective force constant . At the equilibrium, the only energy is kinetic energy so
By using a frame of reference where the center of mass of the molecule is constant, the total momentum must be zero. Therefore , meaning
where
This represents the system as if it were a single mass moving with momentum . The can be thought of as an effective mass, known as the reduced mass, and it is used when dealing with the vibration of the molecule.
Note: when the masses are the same, , which makes sense because the atoms both move equally. In a situation where one atom is much greater mass than the other, the reduced mass is about equal to the smaller mass (since the larger atom has significant inertia).