Rutherford Scattering
Saturday, February 5, 2022
Rutherford's Observations
While observing the scattering of alpha-particles in atoms, Rutherford realized the equally-distributed positive charge Thomson proposed was unlikely. Instead, Rutherford proposed a small region (called the nucleus) or an atom where the positive charge is.
Repulsive force
For a projectile of charge , the nucleus hypothesis would predict a repulsive force as such:
With the nucleus theory, particles always experience the full positive charge of the atom, unlike in the Thomson model.
Scattering
Particle projectiles follow hyperbolic paths passing by the nucleus of atoms, according to the following equation in polar coordinates:
Since the particle begins at and and the final position is and , the previous equation can be reduced to
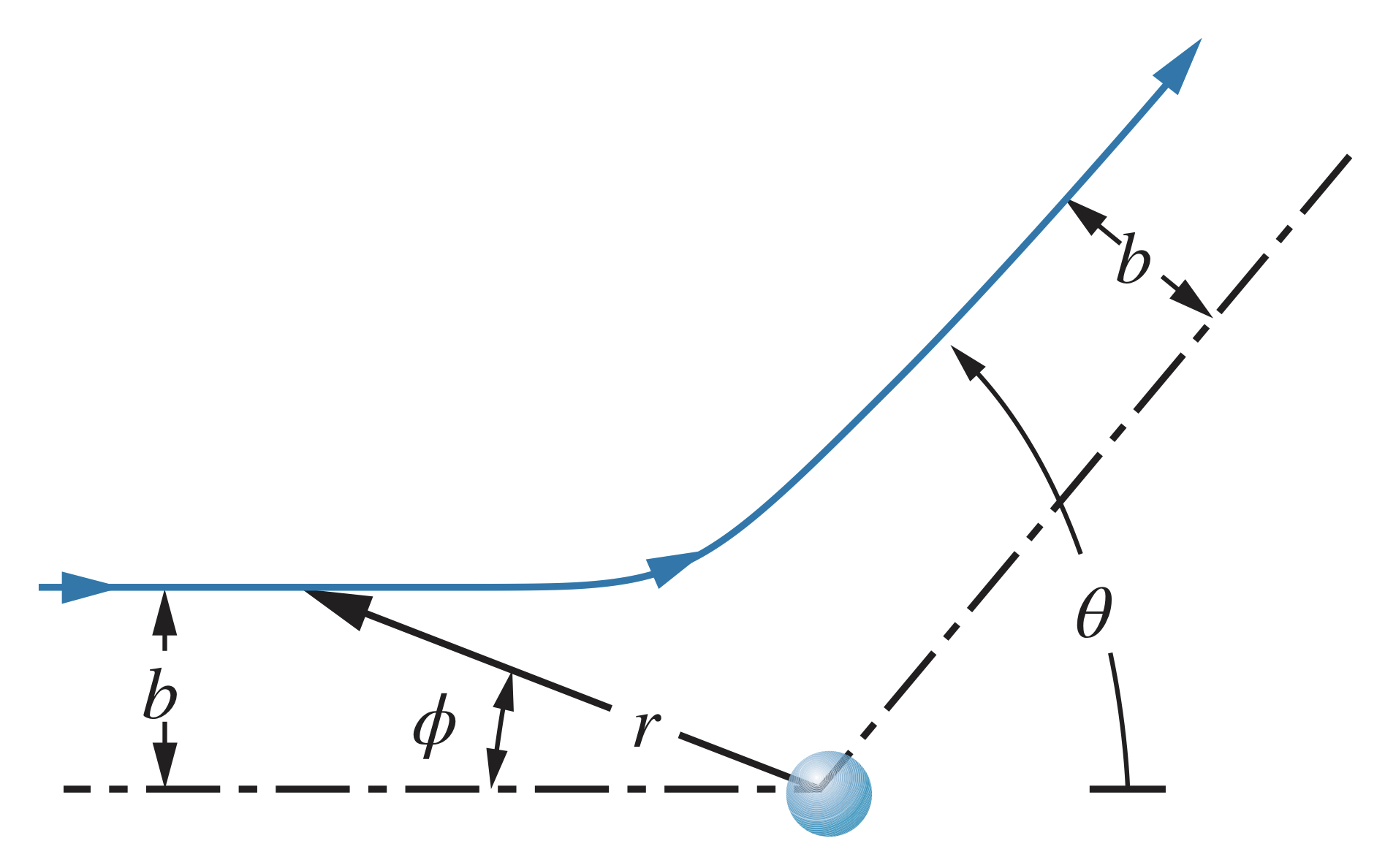
The constant term is equal to eV * nm.
The larger the distance , the less the particle will be scattered. The closer the particle comes to the nucleus (smaller ), the more it will be scattered.
Rutherford Scattering
Some projectiles scatter at angles greater than
For a foil of atoms, one atom thick, the total area is . For the scattering to be greater than , the impact parameter must be between and .
Therefore, the probability of the projectile falling within that range is .
For foils greater than one atom thick, say thickness with area, density, and molar mass, the volume of the foil is , the mass , and number of moles . The number of atoms (and therefore nuclei) per unit volume is
where is Avogadro's number. Using this, the fraction of projectiles scattered at angles of less than is
Experimental verification
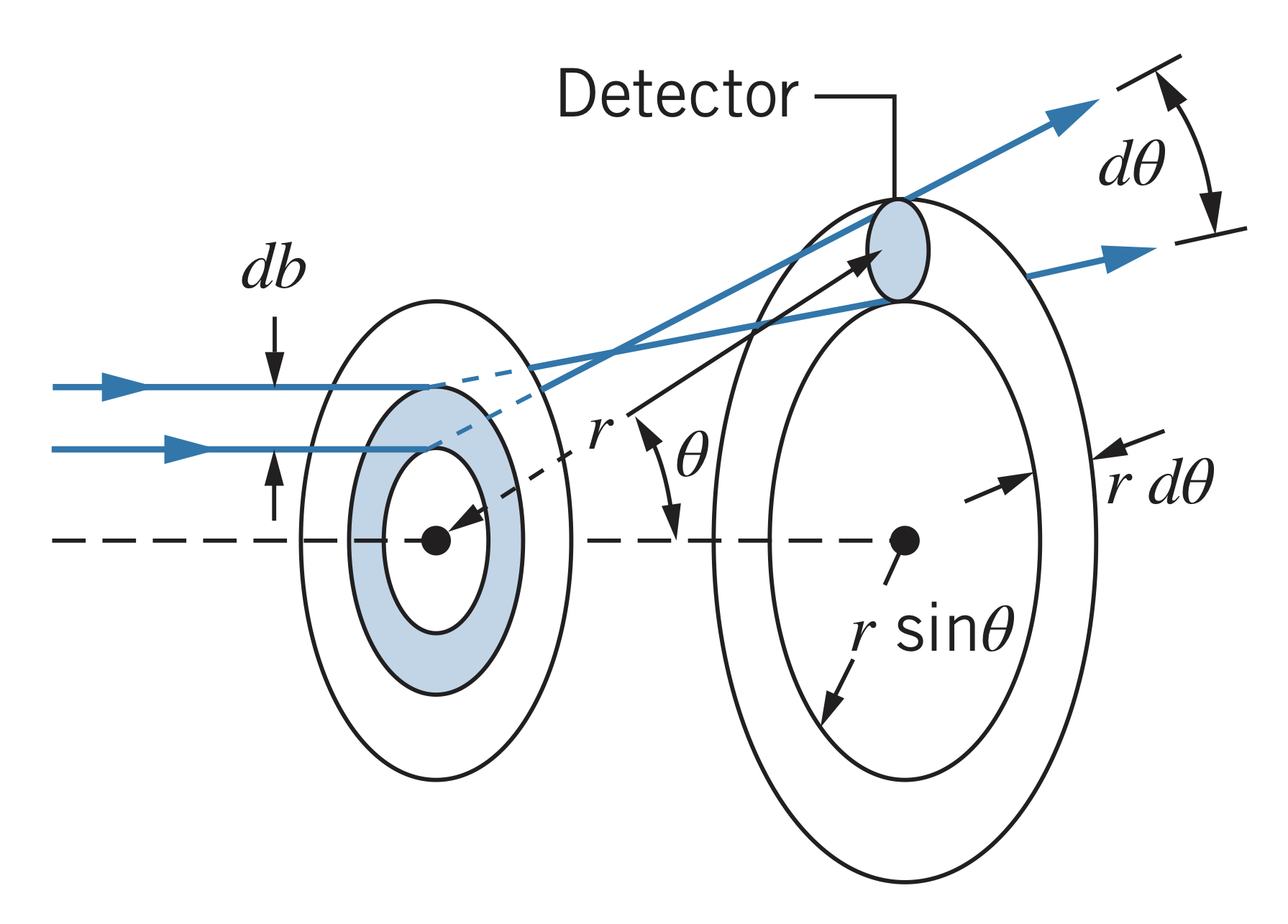
To find the fraction of particles scattered within a small range (between and ), the impact parameter must be between and . The fraction, , is then
Using the previous equation for , however, can be calculated to be
Therefore,
The Rutherford scattering formula, which is the probability per unit area for scattering into the ring, is
Closest approach to the nucleus
As a projectile approaches the nucleus, its kinetic energy is transformed into electrostatic potential energy since
The maximum potential energy occurs when the kinetic energy is lowest (since energy is conserved), which occurs at a distance of and velocity of :
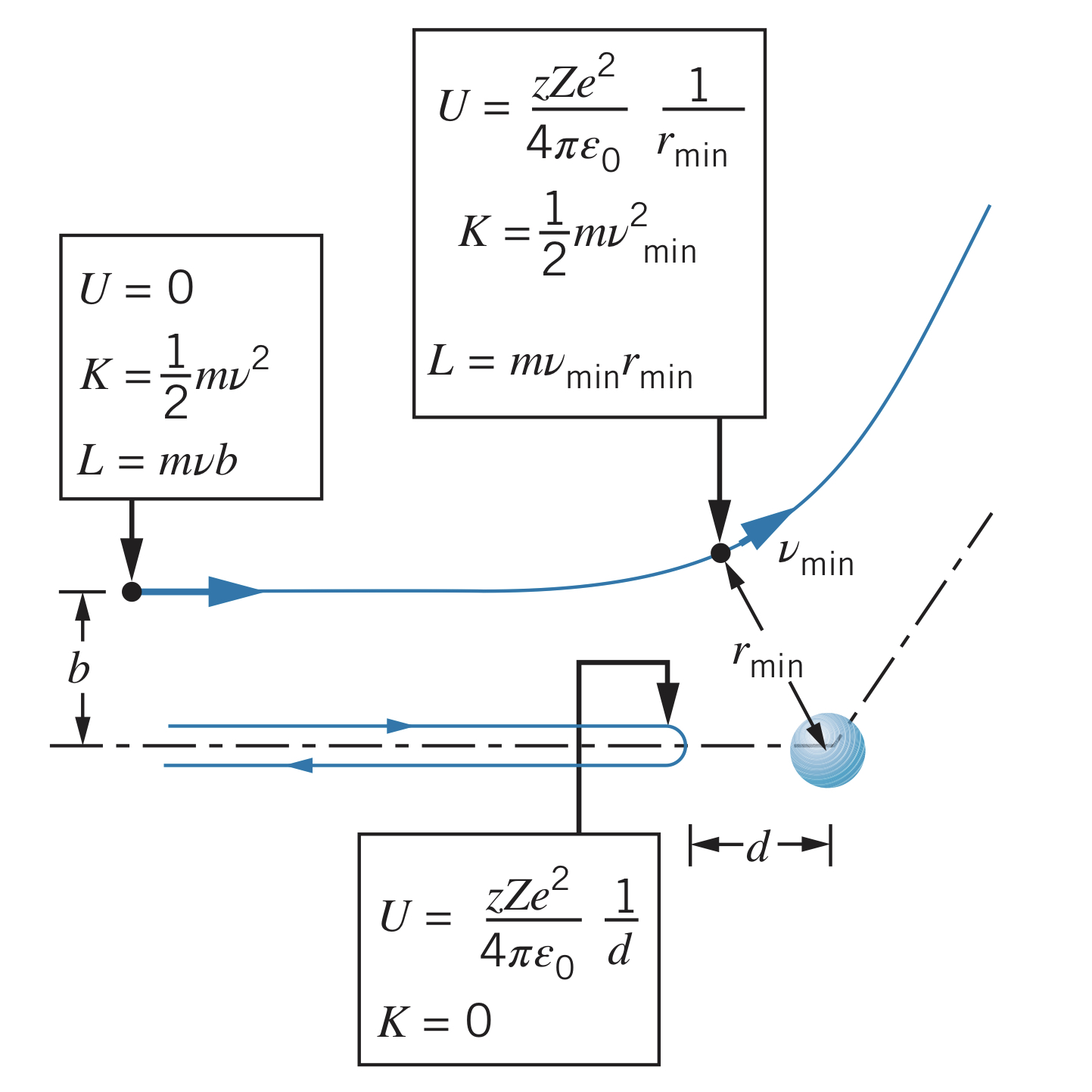
Since angular momentum, , is also conserved, the angular momentum is
Therefore, , so
Since the kinetic energy is not at unless , the closest approach, , is
The Rutherford scattering law predicts a very small radius for the minimum distance, but it is not always greater than the nuclear radius for large values of or low values of . In that case, the particle no longer experiences the full force of the nucleus and so the Rutherford scattering law does not apply.