Radioactive Decay
Sunday, April 3, 2022
Stable Nuclei
In small atoms, nuclei with equal numbers of neutrons and protons are quite stable, but as the atomic number increases, more neutrons are required to separate the protons due to the growing Coulomb repulsion factor of .
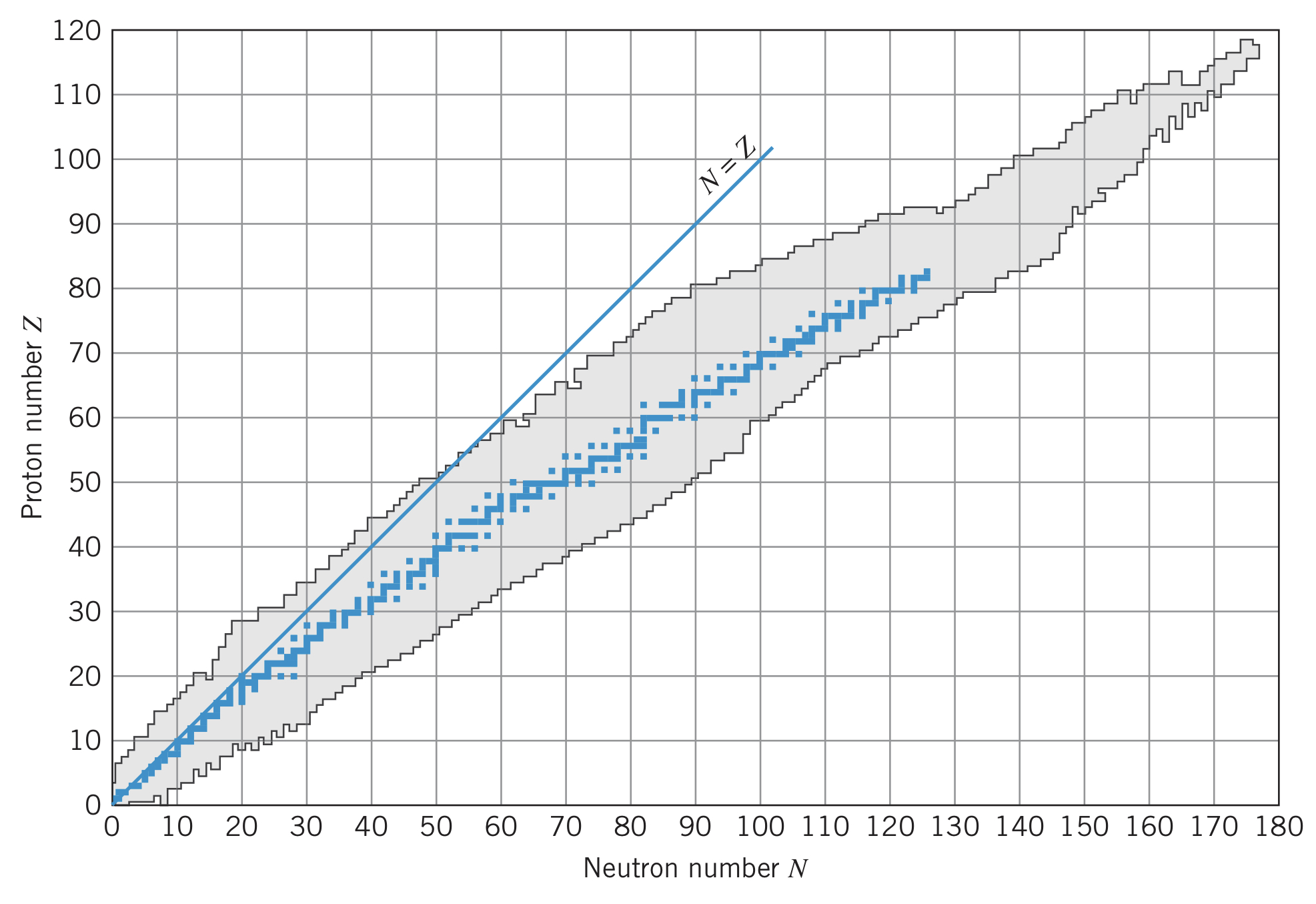
Most of the nuclei in the image above are unstable, meaning they transform themselves into more stable nuclei in one of three processes:
- Nuclei can emit to change their and (called alpha decay)
- Nuclei can change a neutron into a proton or proton into a neutron (called beta decay)
- Nuclei in excited states can emit photons to transition to ground states (called gamma decay)
These processes are called radioactive decay.
Rate of Radioactive Decay
The rate at which radioactive nuclei decay in a sample is called the activity of a sample. The greater the activity, the more nuclear decays per second. Activity is measured in the curie, where
In a radioactive substance, the probability any given nucleus decays is equal to its activity divided by the number of radioactive nuclei. This decay probability is called the decay constant, denoted . In other words, an activity depends on the number of radioactive nuclei and the decay constant :
But as the substance decays, there are fewer radioactive nuclei. Therefore, we can regard as the change in the number of radioactive nuclei per unit time:
Combining this with the expression of activity above, we see
Integrating, we get
where is the number of nuclei originally present at . This is called the exponential law of radioactive decay. Since it can be difficult to measure , we can multiply both sides by to get
where is the original activity.
Half-life
The half-life, , of the decay is the time it takes for the activity to be reduced by half. Therefore, when , , so
The mean lifetime, , is defined as
where when , .
Conservation Laws
Certain universal laws (called conservation laws) limit the types of radioactive decay that can happen.
Conservation of energy
The conservation of energy allows us to determine which types of decay are energetically possible and allows calculations of the rest energies and kinetic energies of decay products.
Say a nucleus decays into a lighter nucleus via the emission of one or particles collectively called . The excess energy, called the value of the decay is
The decay is only possible if is positive. That excess energy appears as kinetic energy of the decay products:
Conservation of linear momentum
Assuming the initial nucleus is at rest, the final linear momentum of the resulting particles must be zero:
Since the particle(s) are typically much less massive than , the recoil momentum yields a very small kinetic energy
Conservation of angular momentum
The total spin angular momentum of the initial particle before the decay must equal the total angular momentum (spin and orbital) of all the products after the decay process.
Conservation of electric charge
The total net electric charge before the decay must equal the net electric charge after the decay.
Conservation of nucleon number
Although particles (like electrons and photons) can be created via the excess energy of the decay process, neutrons and protons cannot be created. Instead, only some processes can convert neutrons to protons and vice versa. That is, the total nucleon number does not change in decay or reaction processes.