Electromagnetic Waves
Saturday, January 22, 2022
Review of Electromagnetism
Electric charges produce an electric field, . Flowing current in a wire produces a magnetic field, . If charges do not move and current does not flow, the electric and magnetic fields are said to be static.
Accelerating charges and currents that vary with time produce electromagnetic waves, where the and fields vary over time.
Electromagnetic Wave Basics
Plane waves
Plane waves (when wave fronts are planes) are the simplest versions of electromagnetic waves. They can be described as such:
Where is the wave number, found from the wavelength: , and is the angular frequency, found from the frequency: .
Since , the wave number and angular frequency are related as such:
Polarization
Polarization is determined by the vector and the direction of propagation of the electromagnetic wave. The direction of must be perpendicular to both and the direction the wave propagates, such that is the direction of the wave.
and are related such that .
Poynting vector,
The electromagnetic wave transmits energy according to its Poynting vector, which is defined as such:
Where is the vacuum permeability constant, approximately .
For the plane wave, the Poynting vector is determined as so:
And since the power received is equal to the energy times area, the power delivered by a plane wave is determined like this:
Or, since ,
Notice how the power delivered is proportional to . This means the intensity, average power per unit area, is proportional to the square of the amplitude of the wave.
Average power
According to the equation above, intensity fluctuates with a frequency of .
Sensors (like our eyes) can't see fluctuations in intensity on the order of times per second. Therefore, we can find the average power as such:
Waves Interacting
Principle of superposition
Waves can interact with each other through the processes of interference and diffraction, because of the principle of superposition, which states that waves can "add together" their amplitudes at points.
Double-slit experiment
A plane wave approaches a wall with two slits in it. On the other side of the wall, the wave is diffracted, such that it covers a greater area than it otherwise would. This causes the waves to interfere with each other, producing a pattern of lines on the screen.
The brighter spots are caused by constructive interference, which is when two waves' crests intersect. The dimmer spots are caused by destructive interference, which is when one wave's crest intersects another wave's trough (valley).
Diffraction Grating
Diffraction grating allows light waves to be split into their constituent wavelengths, according to the following equation:
Where is the slit spacing and is the order of diffraction (an integer), which represents which set of wavelengths of light the angle refers to (see image below).
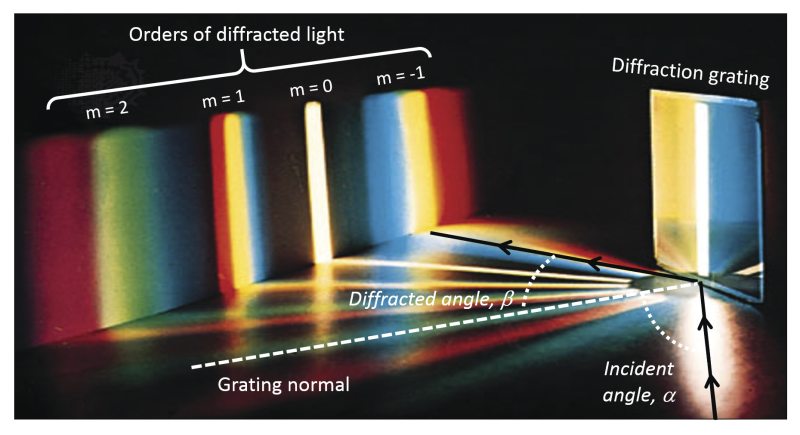
Diffraction grating is useful if is only a few times the wavelength, making it impossible for short-wavelength light like x-rays.
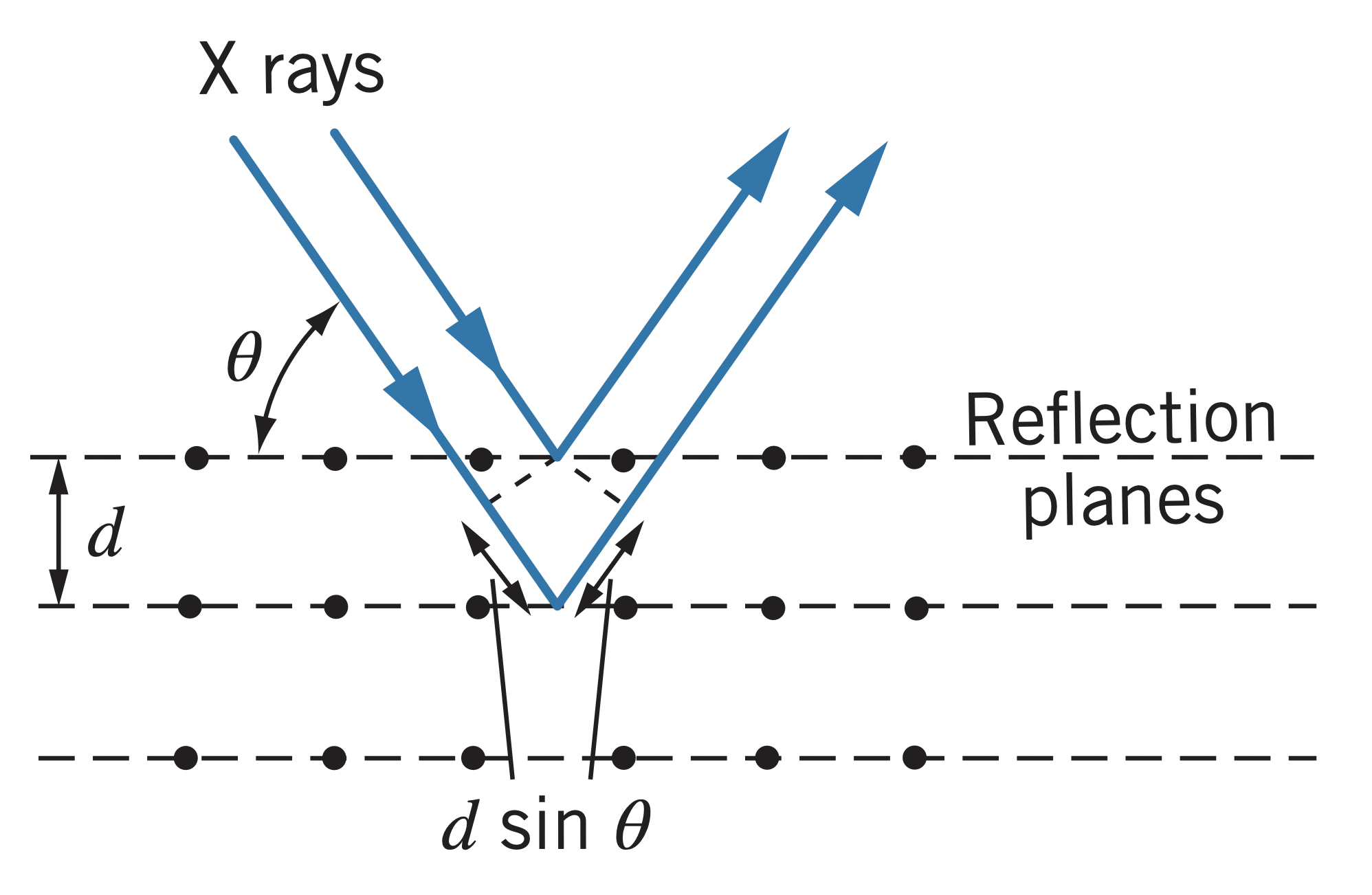
X-ray crystal diffraction
For short wavelength light, crystalline structures of materials are used to diffract the light. Interference maxima occur according to Bragg's Law of X-ray Diffraction: