← Wave Mechanics

Wave Packets

Friday, February 11, 2022

Traveling Waves

Wave packets are traveling waves, which move through space with some uniform speed. Pictures only show wave packets at one instant in time, so a part of the wave that looks like it has no displacement will if the wave is moving.

Constructing a Wave Packet

Waves can be added together to form a wave packet, forming a localized region of space that the wave takes up. Adding together two waves of amplitude $A$ and wave number $k$ ($k=2\pi/\lambda$) gives the function

$$y\left(x\right)=A_1\cos{\left(k_1x\right)}+A_2\cos{\left(k_2x\right)}=A_1\cos{\left(2\pi x/\lambda_1\right)}+A_2\cos{\left(2\pi x/\lambda_2\right)}$$

A phenomenon called beats occurs when sound waves of different frequencies are added. However, since we are still adding the waves from $-\infty$ to $+\infty$, there is no localized wave packet. Adding more waves, of increasing wavelength, would result in a narrower pulse resembling a wave packet, but it still continues forever in the $-\infty$ and $+\infty$ directions.

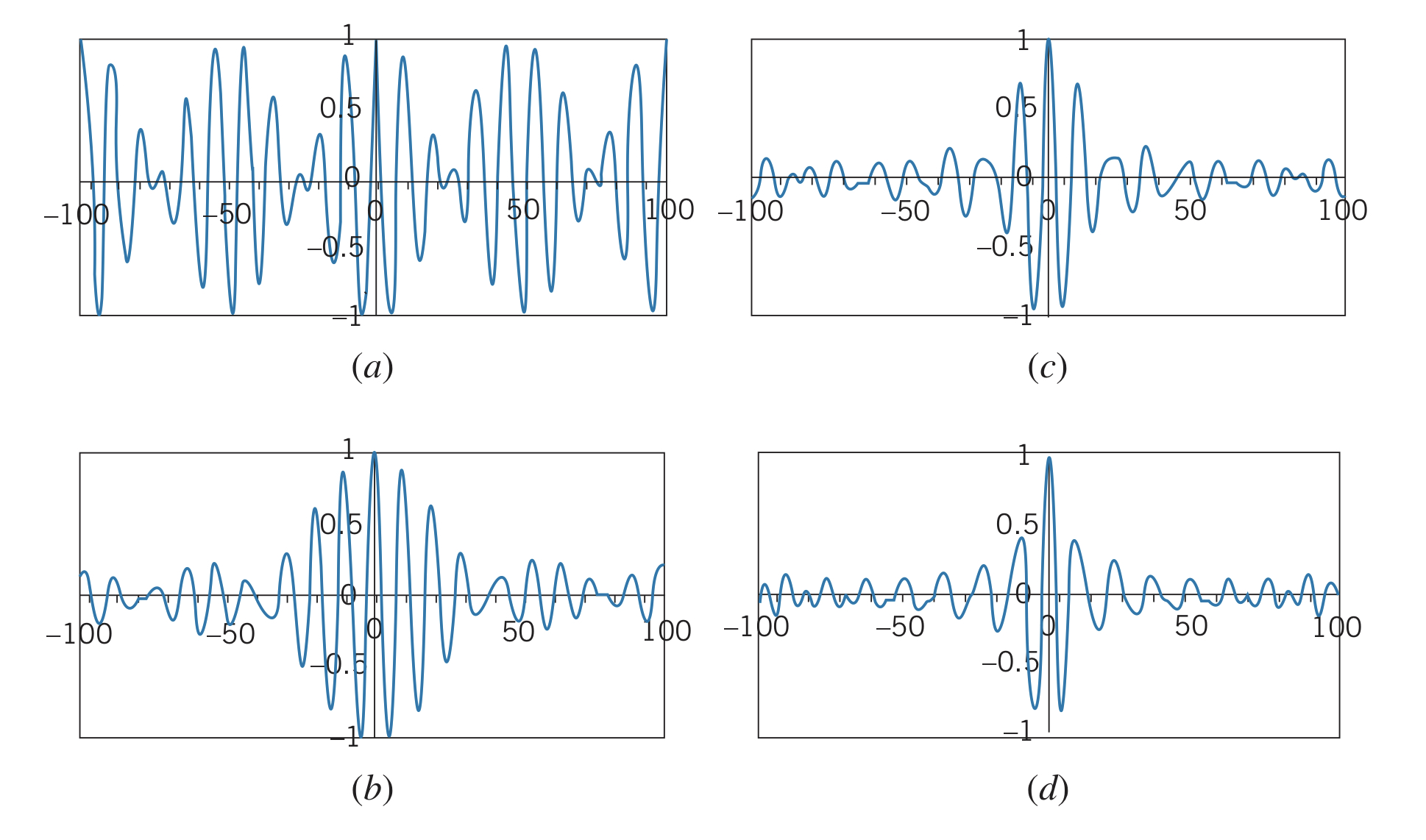
Notice that as more waves are added, the "wave packet" gets narrower, resembling the inverse relationship between location certainty and wavelength certainty.

For two waves of the same amplitude, $A=A_1=A_2$, the summed waves can be written as:

$$y\left(x\right)=2A\cos\left(\frac{\pi x}{\lambda_1}-\frac{\pi x}{\lambda_2}\right)\cos\left(\frac{\pi x}{\lambda_1}+\frac{\pi x}{\lambda_2}\right)$$

And if the wavelengths are close to each other ($\Delta \lambda=\lambda_2-\lambda_1{\lt\lt}\lambda_1,\lambda_2$), the equation can be approximated as:

$$y\left(x\right)=2A\cos\left(\frac{\Delta \lambda \pi x}{\lambda_{av}^2}\right)\cos\left(\frac{2\pi x}{\lambda_{av}}\right)$$

However, this still results in an infinite wave packet. Two approximations for finite wave packets are:

$$y\left(x\right)=\frac{2A}{x}\sin\left(\frac{\Delta \lambda \pi x}{\lambda_0^2}\right)\cos\left(\frac{2\pi x}{\lambda_0}\right)\newline y\left(x\right)=Ae^{-2\left(\Delta \lambda \pi x / \lambda_0^2\right)^2}\cos\left(\frac{2\pi x}{\lambda_0}\right)$$

Adding waves of differing amplitudes and wavelength

Another approach is adding waves of different amplitudes and wavelengths (although wave numbers are more convenient: $k=2\pi/\lambda$):

$$y\left(x\right)=\sum A_i\cos{k_ix}$$

And summing over a continuous set of wave numbers gives

$$y\left(x\right)=\int A\left(k\right)\cos{kx}~dk$$